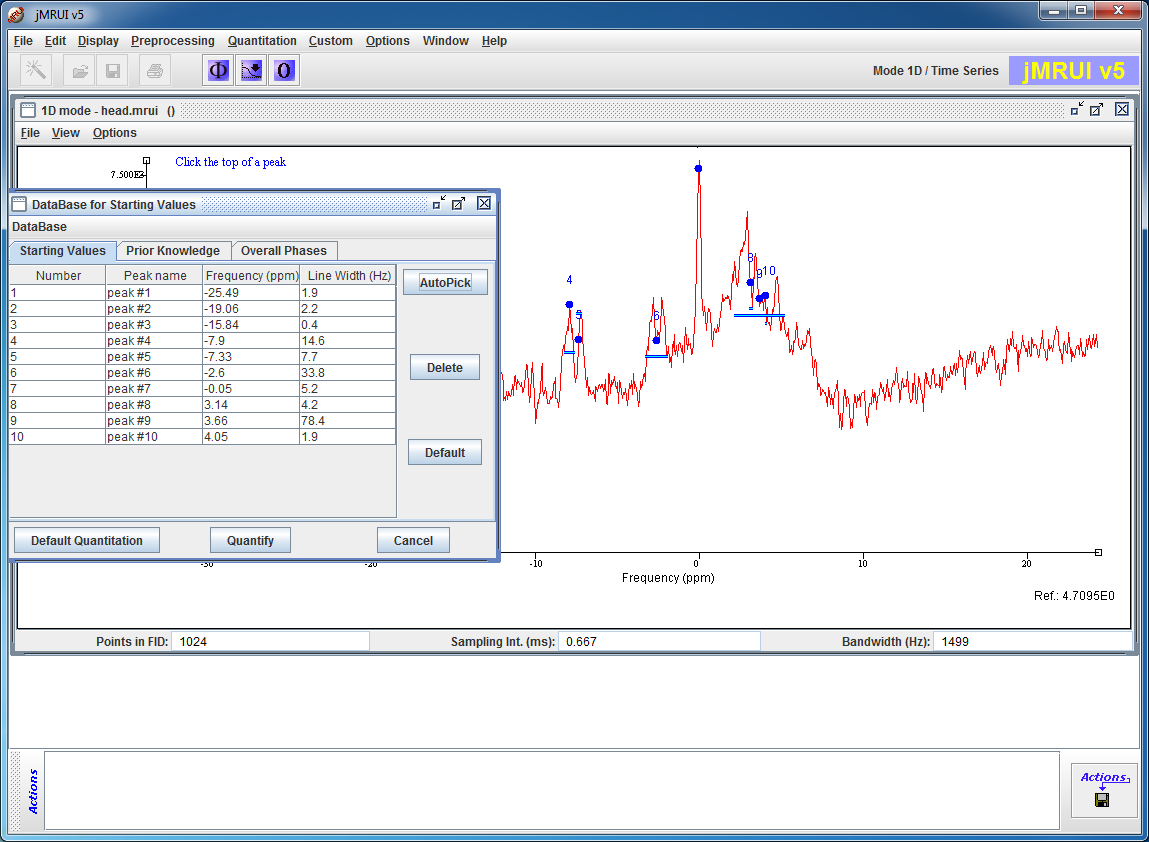
jMRUI includes several quantitation algorithms. Some of them are listed below:
SVD based algorithms
The non-interactive black box algorithms based on Singular Value Decomposition (SVD) are efficient for quantitating signals with good signal-to-noise ratios. They are also helpful in parametrizing signals of unknown composition and shape, but they cannot make use of all available prior knowledge.
HLSVD
The Hankel Lanczos Squares Singular Values Decomposition (HLSVD) is a very fast black box quantitation method based on the Lanczos algorithm.
HTLS
LPSVD
The Linear Prediction Singular Value Decomposition (LPSVD) quantitation method is not very quick, but allows up to 99 components in the estimated signal. The number of points allowed in the quantitation is limited to 1024. This method is less robust than HLSVD and if LPSVD yields incoherent results, try to truncate some points at the signal beginning.
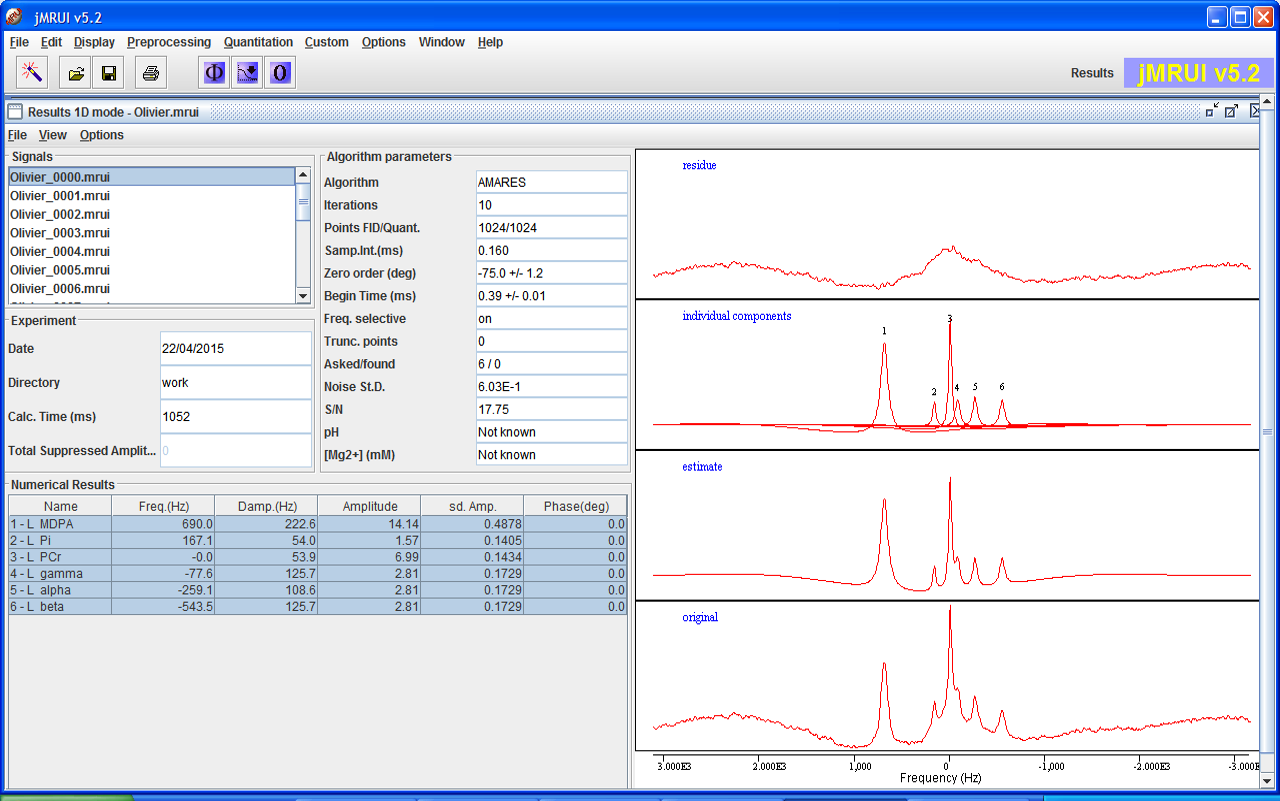
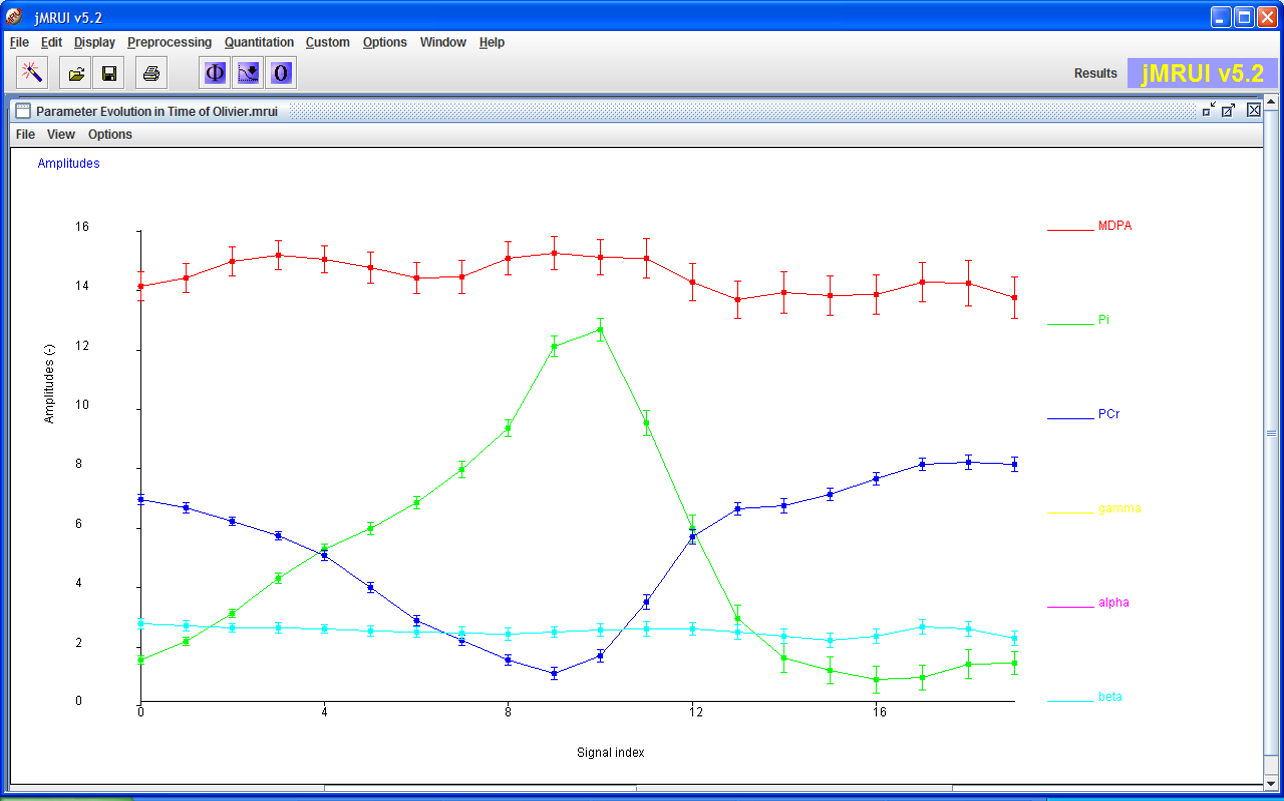
AMARES
AMARES is a non-linear-least-squares (NLLS) quantitation algorithm that demands more user interaction compared to the black box methods. The user can provide constraints to some components and introduce some Prior Knowledge that can improve the precision of the quantitation.
References
- AMARES – Vanhamme, L., van den Boogaart, A., Van Huffel, S. Improved method for accurate and efficient quantification of MRS data with use of prior knowledge. Journal of Magnetic Resonance 129: 35-43, 1997.
- Danielle Graveron-Demilly. Quantification in magnetic resonance spectroscopy based on semi-parametric approaches. Magnetic Resonance Materials in Physics, Biology and Medicine, pages 1– 8, 2013. ISSN 0968-5243. doi: 10.1007/s10334-013-0393-4. URL http: //dx.doi.org/10.1007/s10334-013-0393-4
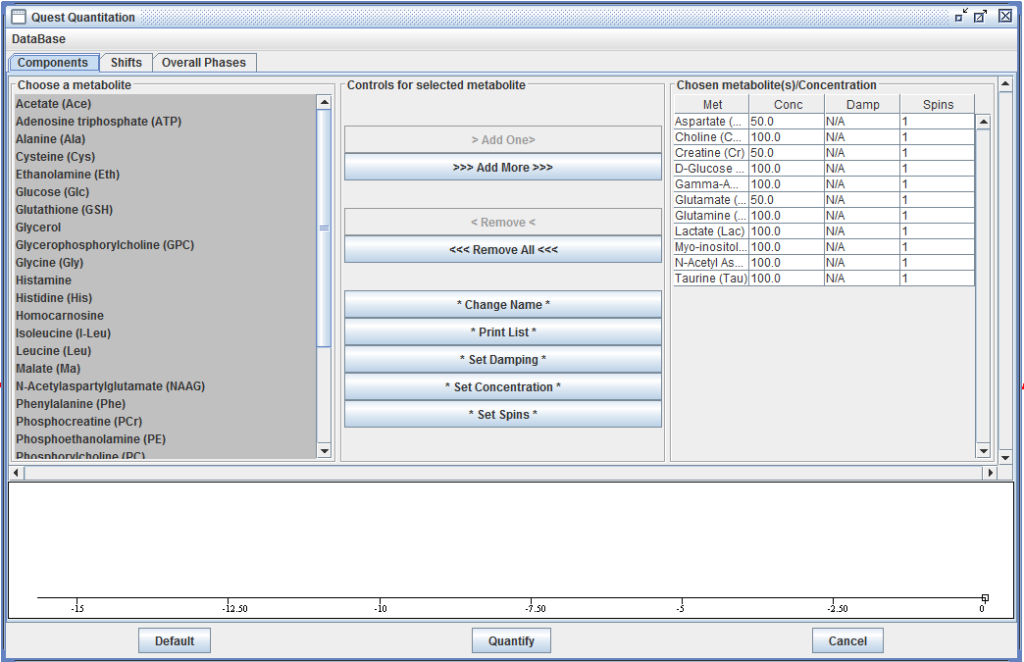
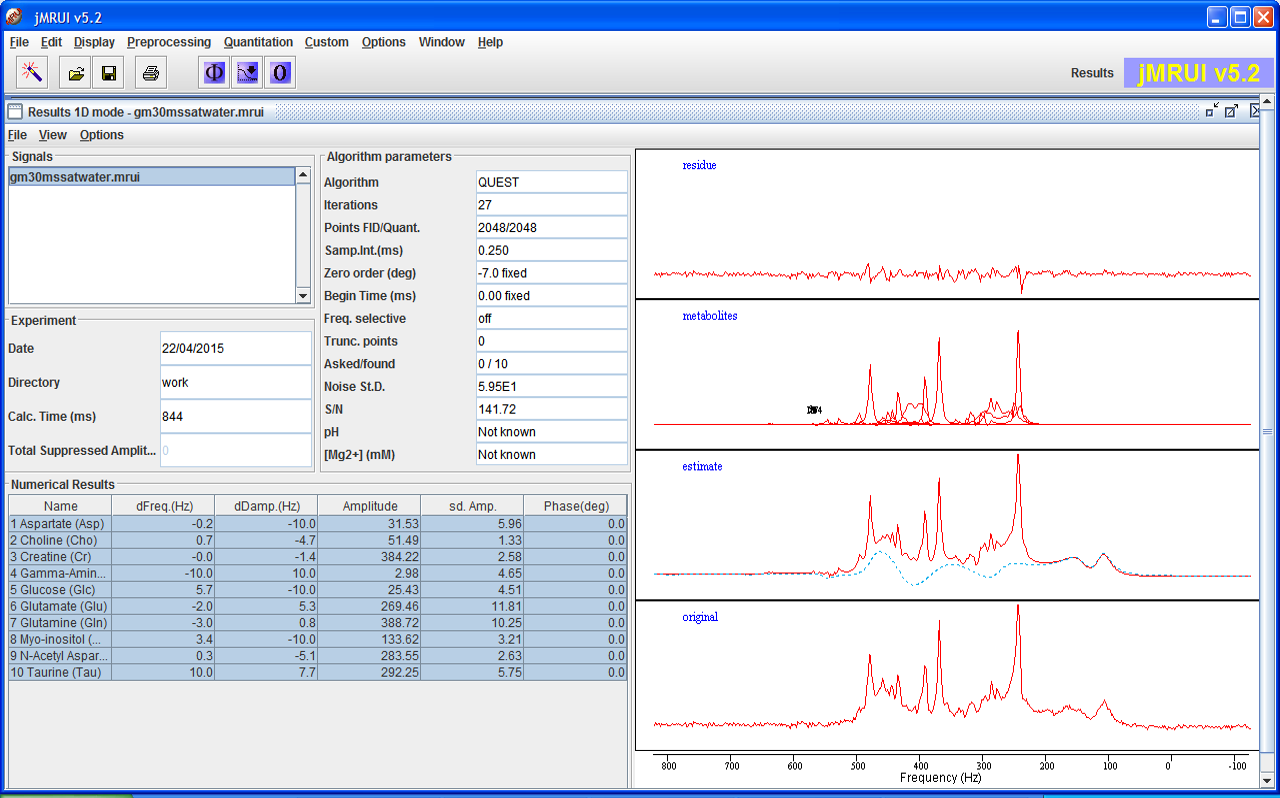
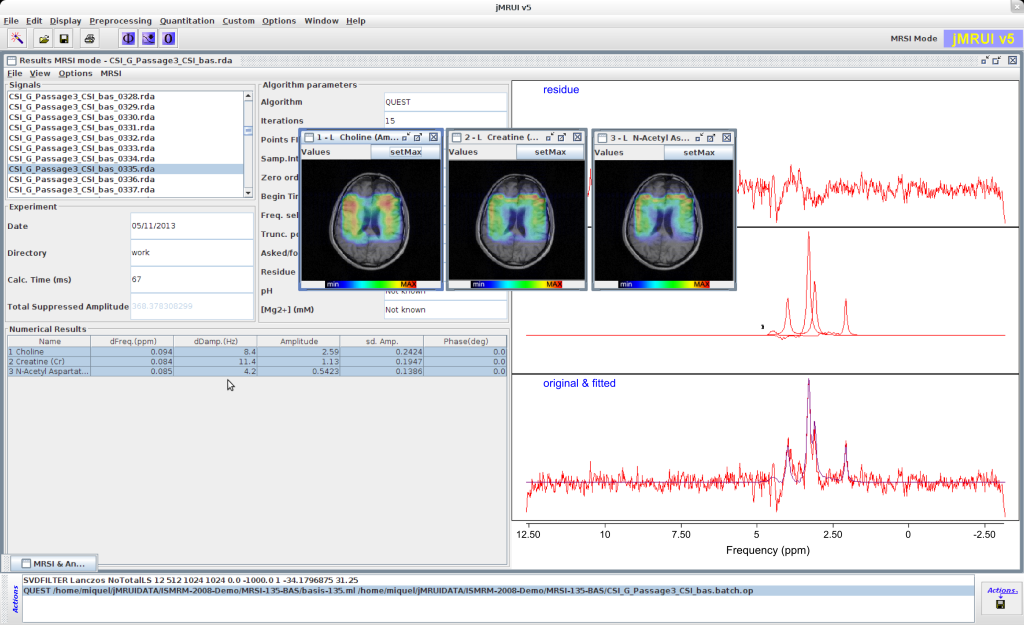
QUEST
QUEST is a time domain algorithm which fits a weighted combination of metabolite signals directly to the in vivo data at hand. It uses advanced prior knowledge based on a metabolite basis set either computed by Quantum Mechanics with NMR-SCOPE or NMRScopeB, or measured in vitro.
References
- Danielle Graveron-Demilly. Quantification in magnetic resonance spectroscopy based on semi-parametric approaches. Magnetic Resonance Materials in Physics, Biology and Medicine, pages 1– 8, 2013. ISSN 0968-5243. doi: 10.1007/s10334-013-0393-4. URL http: //dx.doi.org/10.1007/s10334-013-0393-4
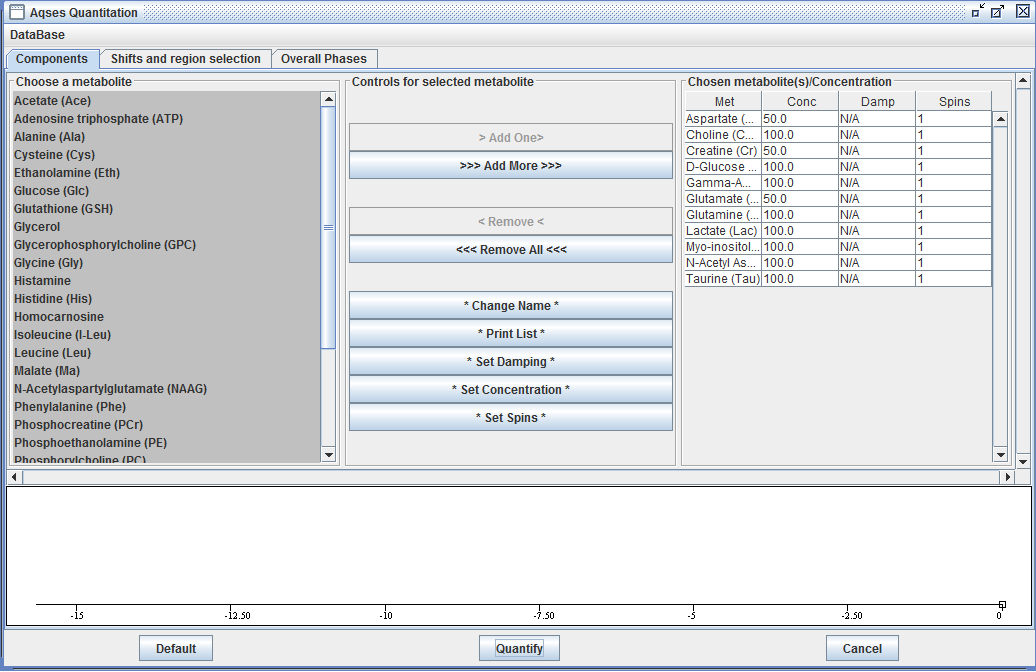
AQSES
AQSES is an algorithm in which the quantitation problem is mathematically formulated as a separable non-linear least-squares fitting problem, which is numerically solved using a modified variable-projection procedure. A macromolecular baseline is incorporated into the fit via non-parametric modelling and is efficiently implemented using penalized splines. Unwanted components such as residual water are removed with a maximum-phase FIR filter. Constraints on the phases, dampings and frequencies of the metabolites can be imposed.
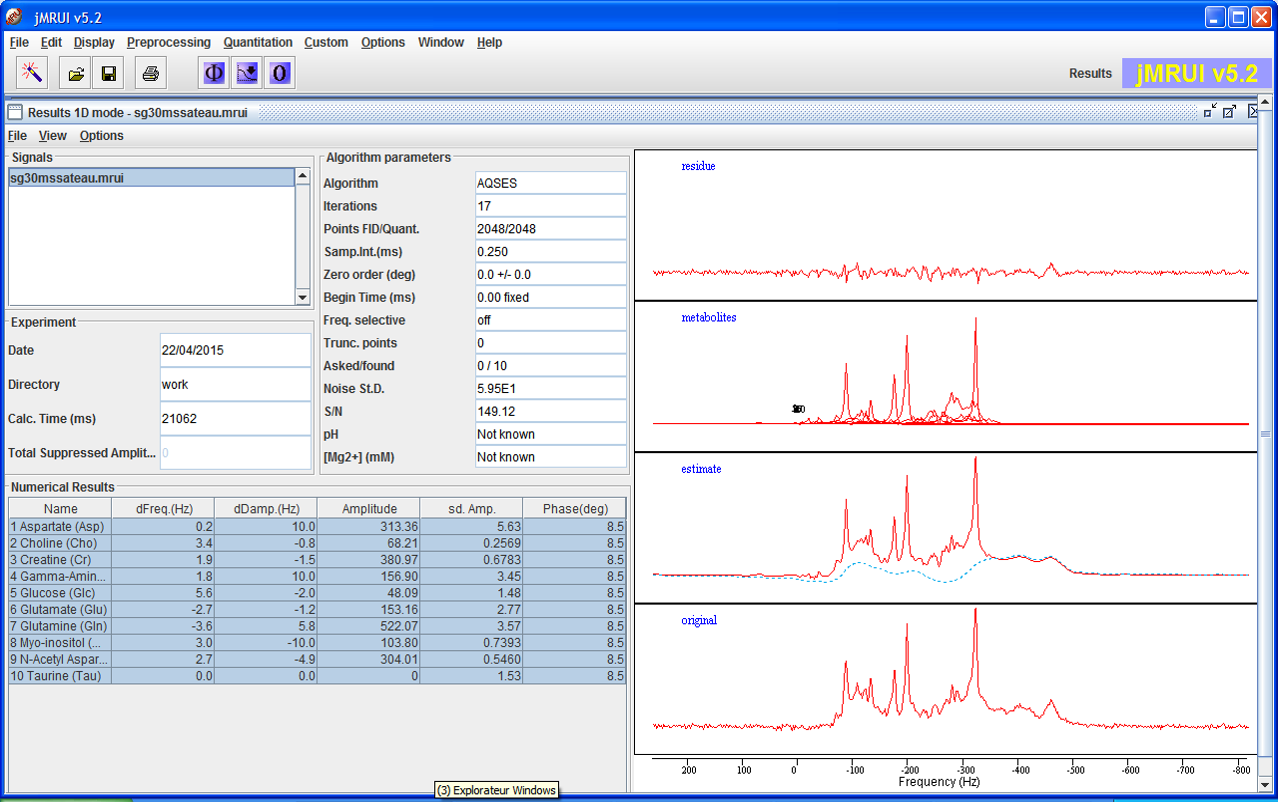
References
- M. Osorio Garcia, Diana Sima, F. Nielsen, U. Himmelreich and S. Van Huffel, Quantification of in vivo Magnetic Resonance Spectroscopy signals with baseline and lineshape corrections
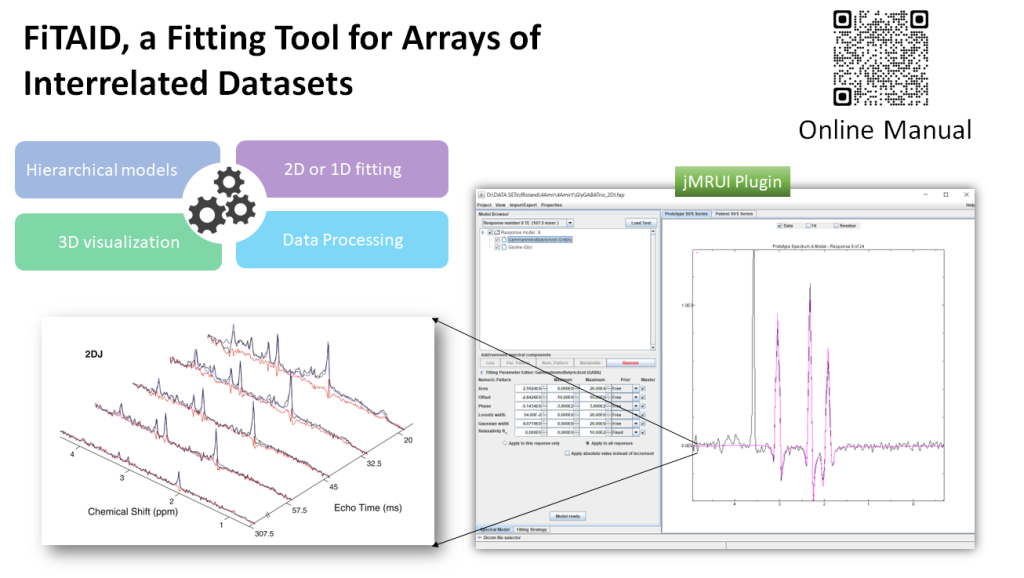
FiTAID is a new plugin integrated to the jMRUI version 7.0 for multidimensional, interrelated spectra quantification. It can be run from the Custom menu. It includes e.g.:
- models for 1D, 2D and multidimensional fitting (Saturation recovery, Inversion recovery, 2DJ, 2DJ diffusion, 2DJIR),
- flexible construction of the signal model with metabolite profiles defined as combinations of simulated signal profile(s) (simulated, e.g., in VeSPA, NMRScopeB (jMRUI)) and/or resonance peaks (Gaussian, Lorentzian, Voigt shapes),
- possibility to set various constraints on estimated parameters,
- possibility to select the fitting strategy (e.g. fitting domain, simultaneous or individual fit, algorithm, fitting region etc.),
- visualization tools for multidimensional data,
- batch processing of large multi-dimensional MRS data.
References
- Chong DGQ, Kreis R, Bolliger CS, Boesch C, Slotboom J. Two-dimensional linear-combination model fitting of magnetic resonance spectra to define the macromolecule baseline using FiTAID, a fitting tool for arrays of interrelated datasets. MAGMA. 2011;24:147–164.
- Adalid V, Döring A, Kyathanahally SP, Bolliger CS, Boesch C, Kreis R. Fitting interrelated datasets: metabolite diffusion and general lineshapes. MAGMA 2017;30(5):429-448.
- For the RANDOM algorithm see: Slotboom J, Hofmann L, Boesch C, and Kreis R. Spectral fitting in a constrained parameter space using a random search strategy and prior knowledge. 6th Meeting of the International Society of Magnetic Resonance in Medicine, Sydney, 1998; p.26